Markov kernel

In probability theory, a Markov kernel is a map that plays the role, in the general theory of Markov processes, that the transition matrix does in the theory of Markov processes with a finite state space.

Formal definition

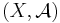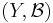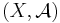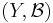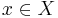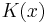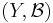Let $(X,\mathcal A)$ , $(Y,\mathcal B)$ be measurable spaces. A Markov kernel with source $(X,\mathcal A)$ and target $(Y,\mathcal B)$ is a map $K$ that associates to each point $x \in X$ a probability measure $K(x)$ on $(Y,\mathcal B)$ such that, for every measurable set 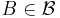$B\in\mathcal B$ , the map 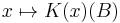$x\mapsto K(x)(B)$ is measurable with respect to the $\sigma$ -algebra 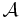$\mathcal A$ .

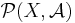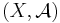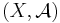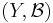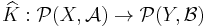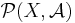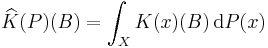Let $\mathcal P(X,\mathcal A)$ denote the set of all probability measures on the measurable space $(X,\mathcal A)$ . 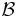If $K$ is a Markov kernel with source $(X,\mathcal A)$ and target $(Y,\mathcal B)$ then we can naturally associate to $K$ a map $\widehat K:\mathcal P(X,\mathcal A)\to\mathcal P(Y,\mathcal B)$ defined as follows: given $P$ in $\mathcal P(X,\mathcal A)$ , we set $\widehat K(P)(B)=\int_XK(x)(B)\,\mathrm dP(x)$ , for all $B$ in $\mathcal B$ .

References

Bauer, Heinz (1996), Probability Theory, de Gruyter, ISBN 3-11-013935-9

§36. Kernels and semigroups of kernels

Reiss, R D (1993), A Course on Point Processes, Springer-Verlag, ISBN 0387979247